
Reproducing Nowak and May's results : the special case of a Maxi-agent society.
Test of The Multi-Agents Plateform
In this appendix we will see the spatial patterns produced by the original model of Nowak & May (1992) This model corresponds to the particular case where the only available law to the agent is Maxi. With the same multi-agents plateform which have been used to study metamimetic dynamics (Matlab), we have thus been able to reproduce Nowak & May's results. We present here the two non trival dynamics displayed by their model, obtained for 1.8<b<2.
| Matrix Game | C | D | Population size : 250 000 |
Self-Interaction | initial distribution of imitation rules: Only Maxi | noise on action: 0 | noise on imitation law update :0 | |
| C | 1 | 0 | ||||||
| D | b | 0 |
The irregular and relatively static Network
When 1.75<b<1.8, the typical asymptotic state is an heterogenous network with a majority of C-agents and lines of D-agents (figure 1).
 |
| Figure 1: Typical asymptotic State for a population composed by only Maxi-agents for b=1.78. The image is a part of a 500x500 toric grid. Here initial condition for behaviors were a random distribution of 90% of C. |
The chaotic Regime
When 1.8<b<2, we can observe a chaotic dynamics with moving C and D clusters (figure 2). The asymptotic frequency fc of C behaviors is caracteristic of this regime. Nowak et May have proposed the theoretical value fc=12log2-8 which is drawn on the graph (figure 3) .
 |
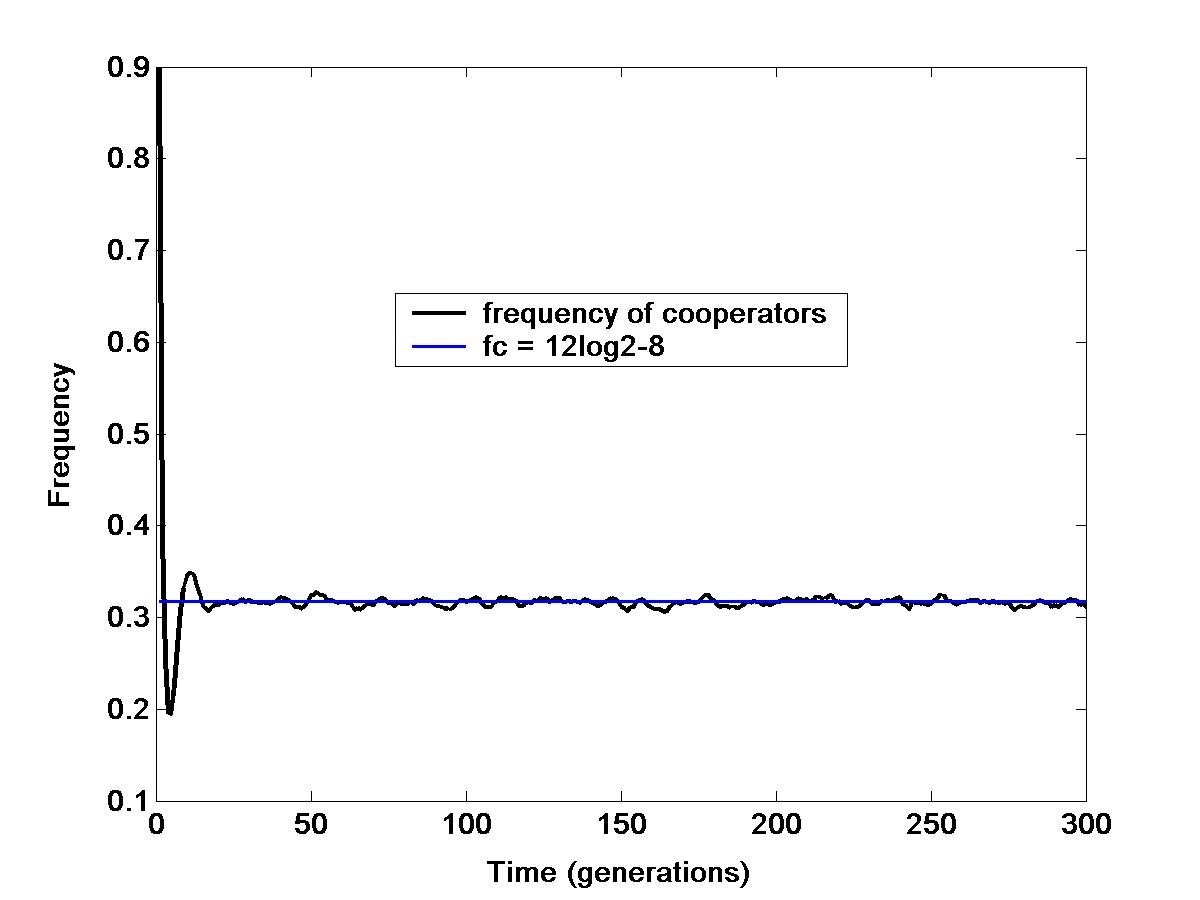 |
| figure 2: Asymptotic State for a population composed by only Maxi-agents for b=1.9. The image is a part of a 500x500 toric grid. C clusters grow in region of D and D clusters grow in region of C. Here initial condition for behaviors were a random distribution of 90% of C. | Figure 3: The evolution of the frequency of cooperators along time in the chaotic regime. The blue line is the theoretical asymptotic value fc=12log2-8 proposed by Nowak et May. |
© David Chavalarias 2003